Mastering Reverse Percentages with Maths Genie: A Comprehensive Guide

Introduction

Reverse percentages are a fundamental concept in mathematics, especially useful when you need to find the original value after a percentage increase or decrease. If you’ve ever wondered how to reverse-engineer a percentage-based calculation, you’re not alone. The good news is that Maths Genie provides excellent resources to make this process easier. In this post, we will walk you through the basics of reverse percentages and show you how to use Maths Genie to master this concept. By the end, you’ll feel confident solving reverse percentage problems on your own.

What Are Reverse Percentages?

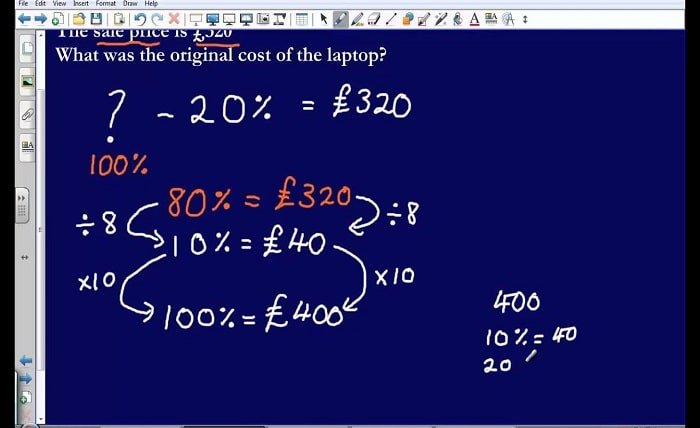
Before diving into the specific tools like maths genie, let’s first define what reverse percentages are. A reverse percentage problem asks you to find the original number before a percentage increase or decrease. For example, if an item costs £120 after a 20% increase, what was the original price? This is where reverse percentages come in handy. Instead of multiplying the original number by a percentage, you’ll need to divide by a percentage or use a formula that takes the percentage into account.

To solve reverse percentage problems, you can use a simple formula:

• Original Value = Final Value ÷ (1 + Percentage Increase)

Understanding reverse percentages is essential because it allows you to deal with everyday financial situations like sales, discounts, or interest rates effectively.

How to Solve Reverse Percentages with Maths Genie

Maths Genie offers a wealth of online tools and resources to help students and learners understand reverse percentages. The platform provides video tutorials, worksheets, and practice questions that make the learning process engaging and effective. To solve reverse percentages on Maths Genie, you simply need to understand the process, apply the relevant formulas, and practice with example problems.

One of the first steps is to break down the problem carefully. Maths Genie emphasizes the importance of understanding what the question is asking before you apply any mathematical steps. The reverse percentage formula can be used in various contexts, including price reductions and calculating original values before VAT (Value Added Tax) is applied.

Key Formula for Reverse Percentages

The reverse percentage formula is a powerful tool for solving these types of problems. Here’s the general equation you’ll use:

• Original Price = Final Price ÷ (1 ± Percentage)

If the percentage increase is involved, you use the “+” sign. For a percentage decrease, you use the “-” sign.

For example, if an item’s price is £150 after a 25% increase, to find the original price:

• Original Price = £150 ÷ (1 + 0.25) = £150 ÷ 1.25 = £120

This is how Maths Genie guides learners in understanding the direct application of the formula. You can experiment with a range of problems to build your confidence and fluency in applying the reverse percentage formula.

Step-by-Step Guide to Solving Reverse Percentage Problems

If you’re looking for a structured approach to solving reverse percentage problems, here’s a step-by-step guide inspired by Maths Genie’s methodical teaching style:

1. Identify the Key Information: Make sure you know the final value and the percentage increase or decrease.
2. Choose the Right Formula: Use the formula for reverse percentages:
   • For percentage increase: Original Price = Final Price ÷ (1 + Percentage)
   • For percentage decrease: Original Price = Final Price ÷ (1 – Percentage)
3. Plug in the Values: Substitute the given values into the formula.
4. Solve the Equation: Perform the calculation to find the original value.
5. Check Your Answer: Ensure that your result makes sense by considering the context of the problem.

This method is efficient and ensures you don’t overlook any critical details in your calculation. Maths Genie helps reinforce this method through interactive examples and worksheets.

Common Mistakes to Avoid When Working with Reverse Percentages

When working with reverse percentages, it’s easy to make mistakes if you’re not careful. Some common errors include:

1. Not understanding the difference between percentage increase and decrease: Always check whether the percentage is adding to or subtracting from the original amount.
2. Incorrect use of the formula: Ensure you’re using the correct formula (either adding or subtracting the percentage).
3. Forgetting to convert percentages to decimals: Before plugging percentages into the formula, you need to convert them into decimal form by dividing the percentage by 100.
4. Not double-checking your answer: After solving, it’s always good practice to verify the result by plugging it back into the problem.

maths genie provides exercises and hints to help you avoid these pitfalls. By practicing regularly, you can hone your skills and improve accuracy.

Real-World Applications of Reverse Percentages

Reverse percentages are commonly used in real-world scenarios such as shopping discounts, tax calculations, and wage adjustments. For instance, if you purchase an item at a sale price and need to find the original price before the discount, reverse percentages can help you. Similarly, if a salary is increased by a percentage, you can use reverse percentages to calculate the original salary before the raise.

Maths Genie helps you see the practical applications of reverse percentages, making abstract concepts more relatable. Whether you’re calculating the price of an item after a discount or determining an original value from a percentage change, reverse percentages are invaluable tools for everyday life.

Conclusion

Mastering reverse percentages can seem daunting at first, but with the right approach and tools like Maths Genie, it becomes manageable. By understanding the key formulas, practicing examples, and avoiding common mistakes, you can confidently solve reverse percentage problems in no time. Maths Genie’s resources offer a step-by-step guide, and with consistent practice, you’ll become proficient in solving reverse percentage problems quickly and accurately.

FAQs

1. What is a reverse percentage?
   • A reverse percentage involves finding the original value before a percentage increase or decrease was applied. It is the inverse process of finding the percentage increase or decrease.
2. How do I calculate a reverse percentage?
   • To calculate a reverse percentage, use the formula:
     • Original Value = Final Value ÷ (1 ± Percentage)
   • For an increase, use “+”; for a decrease, use “-“.
3. Can Maths Genie help me with reverse percentages?
   • Yes! Maths Genie offers a variety of resources, including tutorials, worksheets, and practice questions to help you understand and solve reverse percentage problems.
4. Why is it important to understand reverse percentages?
   • Reverse percentages are useful in real-life situations like calculating discounts, tax rates, and price changes. They also form a key part of many financial and business calculations.
5. What are some common mistakes when solving reverse percentage problems?
   • Common mistakes include forgetting to convert percentages into decimals, using the wrong formula, and not checking the answer to ensure its correctness.